Multidimensional data

Last updated on 2024-01-26 | Edit this page

Overview

Questions

How can we use scikit-image to perform image processing tasks on multidimensional image data?
How can we visualise the results using Napari?

Objectives

Learn about multidimensional image data such as 3D volumetric stacks and timelapses.
Visualize multidimensional data interactively using Napari.
Learn to use the basic functionality of the Napari user interface including overlaying masks over images.
Construct an analysis workflow to measure the properties of 3D objects in a volumetric image stack.
Construct an analysis workflow to measure changes over time from a timelapse movie.

In this episode we will move beyond 2D RGB image data and learn how to process and visualise multidimensional image data including 3D volumes and timelapse movies.

Unofficial episode

This additional episode is not part of the official Carpentries Image Processing with Python Lesson. It was developed by Jeremy Pike from the Research Software Group and the Institute for Interdisciplinary Data Science and AI at the University of Birmingham.

First, import the packages needed for this episode

PYTHON

import imageio.v3 as iio
import skimage as ski
import numpy as np
import napari
import matplotlib.pyplot as plt

%matplotlib
widget

What is multidimensional image data?

Image data is often more complex than individual 2D (xy) images and can have additional dimensionality and structure. Such multidimensional image data has many flavours including multichannel, 3D volumes and timelapse movies. It is possible to combine these flavours to produce higher n-dimensional data. For example a volumetric, multichannel, timelapse dataset would have a 5D (2+1+1+1) structure.

Multichannel image data

In many applications we can have different 2D images, or channels, of the same spatial area. We have already seen a simple example of this in RGB colour images where we have 3 channels representing the red, green and blue components. Another example is in fluorescence microscopy where we could have images of different proteins. Modern techniques often allow for acquisition of more than 3 channels.

3D volumetric data

Volumetric image data consists of an ordered sequence of 2D images (or slices) where each slice corresponds to a, typically evenly spaced, axial position. Such data is common in biomedical applications for example CT or MRI where it is used to reconstruct 3D volumes of organs such as the brain or heart.

Timelapse movies

Timelapse movies are commonplace in everyday life. When you take a movie on your phone your acquire an ordered sequence of 2D images (or timepoints/frames) where each image corresponds to a specific point in time. Timelapse data is also common in scientific applications where we want to quantify changes over time. For example imaging the growth of cell cultures, bacterial colonies or plant roots over time.

Interactive image visualisation with Napari

In the previous episodes we used matplotlib.pyplot.imshow() to display images. This is suitable for basic visualisation of 2D multichannel image data but not well suited for more complex tasks such as:

Interactive visualisation such as on-the-fly zooming in and out, rotation and toggling between channels.
Interactive image annotation. In the Drawing episode we used functions such as ski.draw.rectangle() to programmatically annotate images but not in an interactive user-friendly way.
Visualising 3D volumetric data either by toggling between slices or though a 3D rendering.
Visualising timelapse movies where the movie can be played and paused at specific timepoints.
Visualising complex higher order data (more than 3 dimensions) such as timelapse, volumetric multichannel images.

Napari is a Python library for fast visualisation, annotation and analysis of n-dimensional image data. At its core is the napari.Viewer class. Creating a Viewer instance within a notebook will launch a Napari Graphical User Interface (GUI) wih two-way communication between the notebook and the GUI:

PYTHON

viewer = napari.Viewer()

The Napari Viewer displays data through Layers. There are different Layer subclasses for different types of data. Image Layers are for image data and Label Layers are for masks/segmentations. There are also Layer subclasses for Points, Shapes, Surfaces etc. Let’s load two RGB images and add them to the Viewer as Image Layers:

PYTHON

colonies_01 = iio.imread(uri="data/colonies-01.tif")
colonies_02 = iio.imread(uri="data/colonies-02.tif")
viewer.add_image(data=colonies_01, name="colonies_01", rgb=True)
viewer.add_image(data=colonies_02, name="colonies_02", rgb=True)
napari.utils.nbscreenshot(viewer)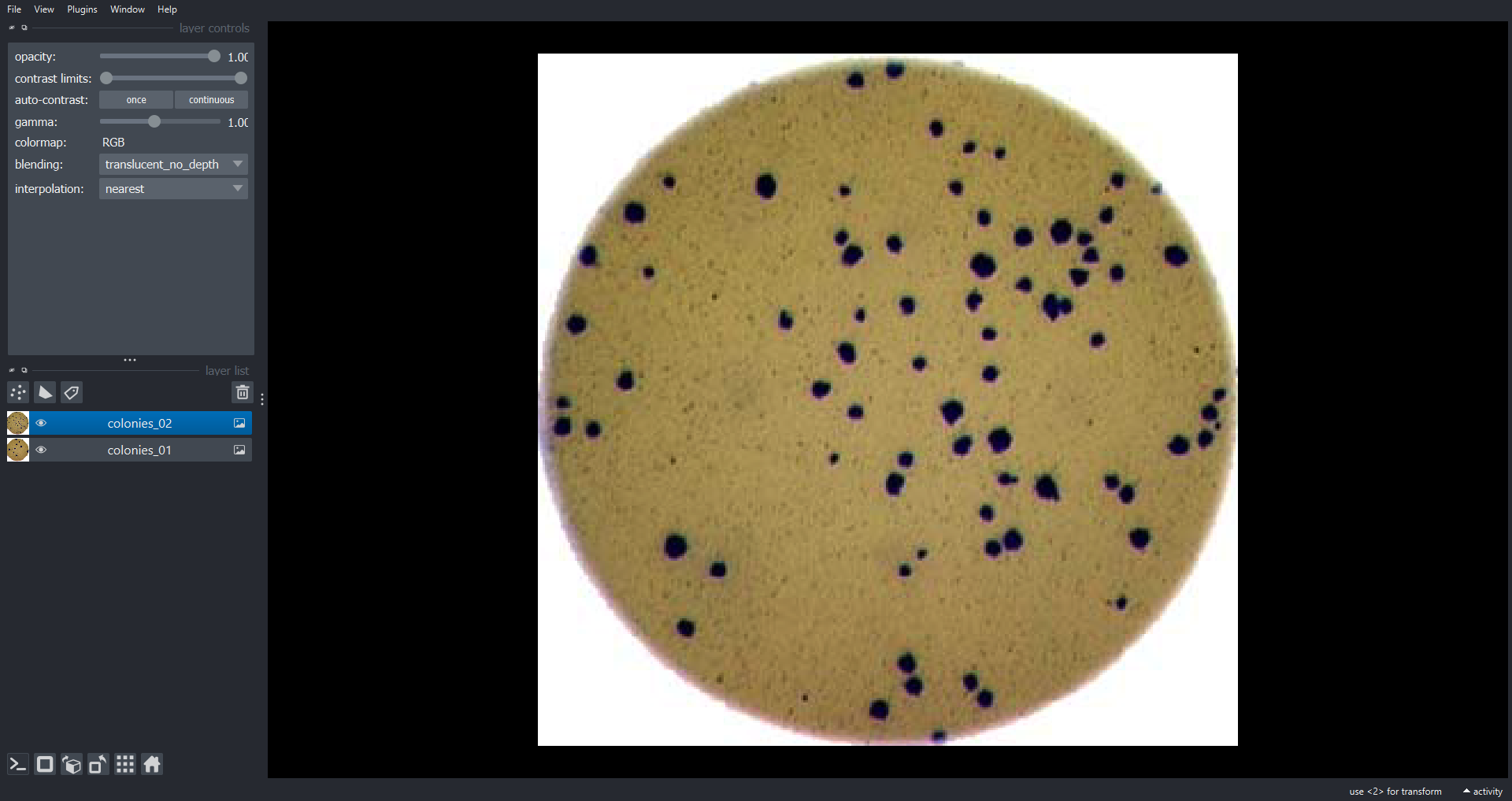

Here we use the viewer.add_image() function to add Image Layers to the Viewer. We set rgb=True to display the three channel image as RGB. The napari.utils.nbscreenshot() function outputs a screenshot of the Viewer to the notebook. Now lets look at some multichannel image data:

PYTHON

cells = iio.imread(uri="data/FluorescentCells.tif")
print(cells.shape)

OUTPUT

(3, 474, 511)

Like RGB data this image of cells also has three channels (stored in the first dimension of the NumPy array). However, in this case we may want to visualise each channel independently. To do this we do not set rgb=True when adding the Image Layer:

PYTHON

viewer.layers.clear()
viewer.add_image(data=cells, name="cells")

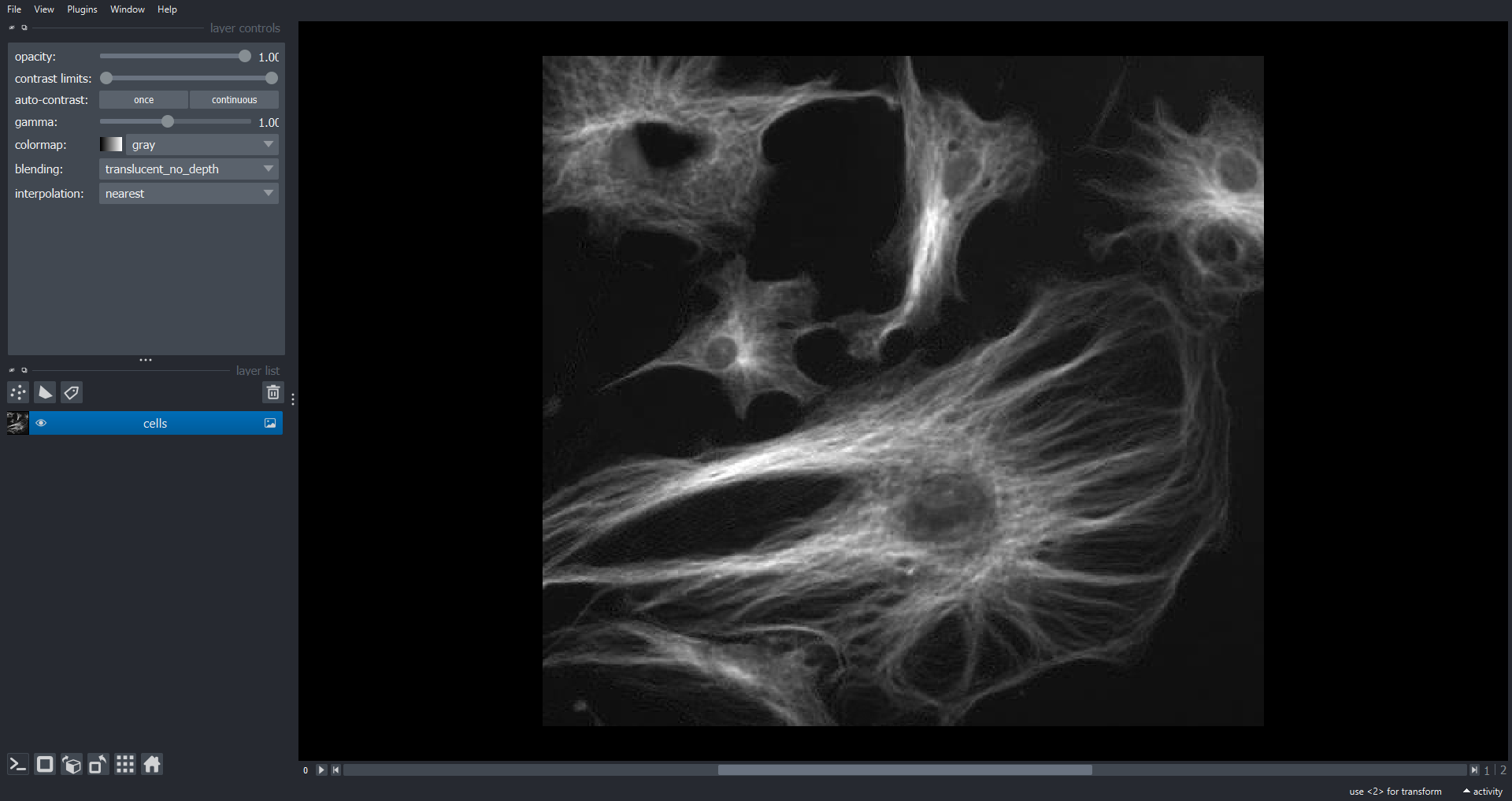
Clearing the Napari Viewer

When we want to close all Layers in a Viewer instance we can use viewer.layers.clear(). This allows us to start fresh, alternatively we could close the existing Viewer and open a new one with viewer = napari.Viewer(). We will use the first approach throughout this Episode but if any point you accidentally close the Viewer you can just open a new one.

We can now scroll through the channels within Napari using the slider just below the image. This approach will work with an arbitrary number of channels, not just three. With multichannel data it is common to visualise colour overlays of selected channels where each channel has a different colour map. In Napari we can do this programmatically using the channel_axis variable:

PYTHON

viewer.layers.clear()
viewer.add_image(data=cells, name=["membrane", "cytoplasm", "nucleus"], channel_axis=0)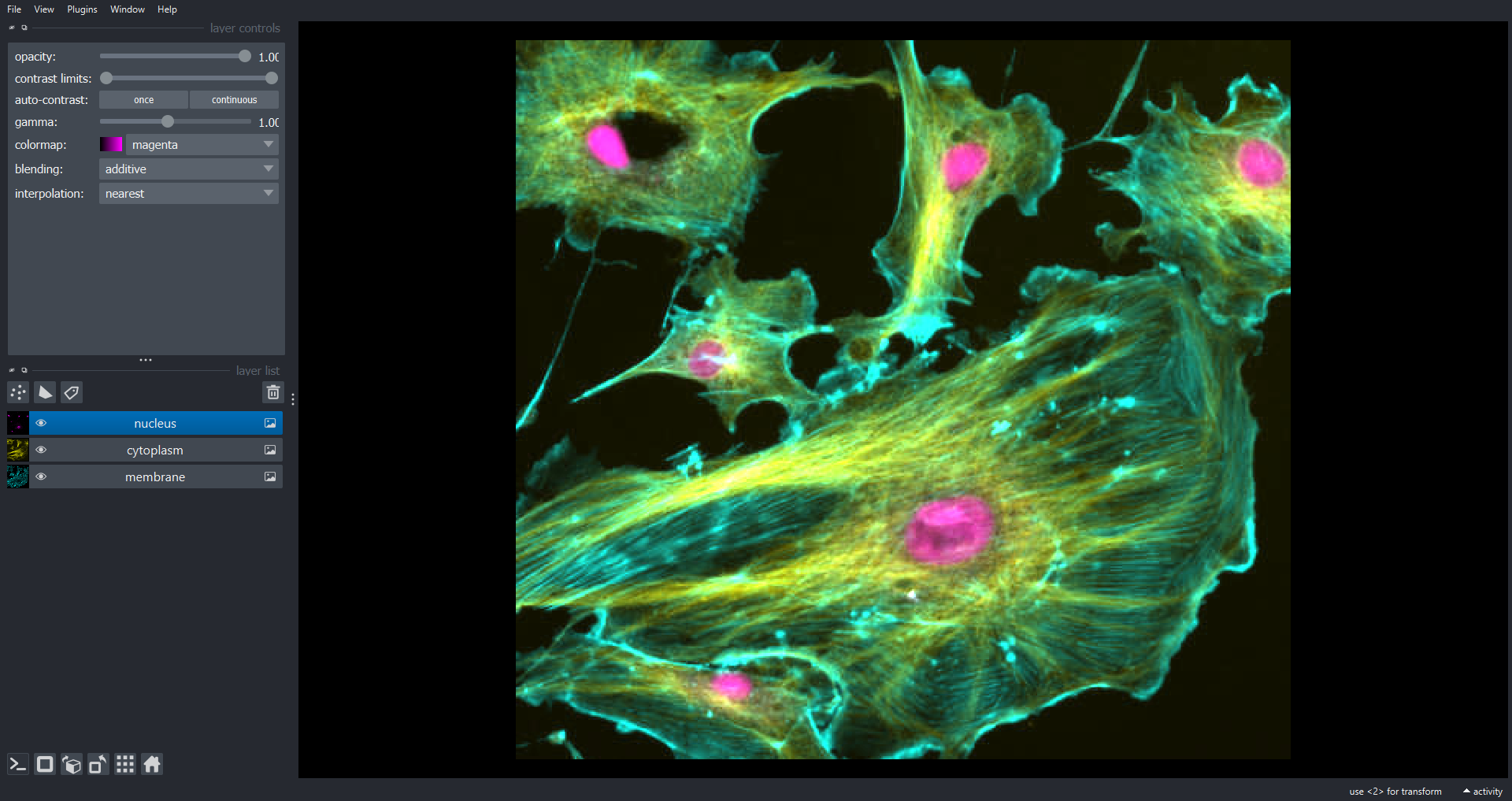

Using what we have learnt in the previous Episodes let’s segment the nuclei . First we produce a binary mask of the nuclei by blurring the nuclei channel image and thresholding with the Otsu approach. Subsequently, we label the connected components within the mask to identify individual nuclei:

PYTHON

blurred_nuclei = ski.filters.gaussian(cells[2], sigma=2.0)
t = ski.filters.threshold_otsu(blurred_nuclei)
nuclei_mask = blurred_nuclei > t
nuclei_labels = ski.measure.label(nuclei_mask, connectivity=2, return_num=False)

Now lets display the nuclei channel and overlay the labels within Napari using a Label layer:

PYTHON

viewer.layers.clear()
viewer.add_image(data=cells[2], name="nuclei")
viewer.add_labels(data=nuclei_labels, name="nuclei_labels")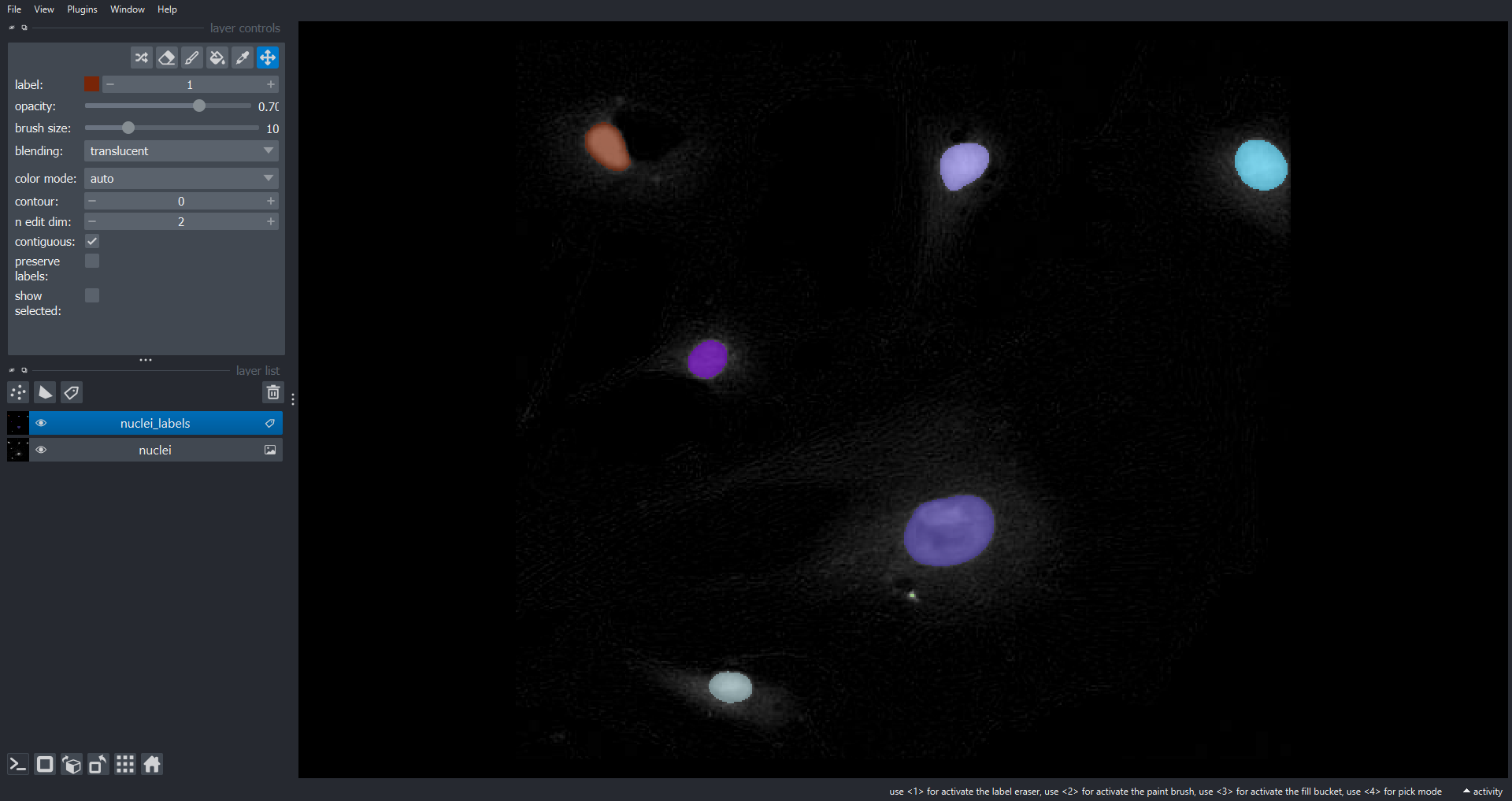

We can also interactively annotate images with shapes using a Shapes Layer. Let’s display all three channels and then do this within the GUI:

PYTHON

viewer.layers.clear()
viewer.add_image(data=cells, name="cells")
# the instructor will demonstrate how to add a `Shapes` Layer and draw around cells using polygons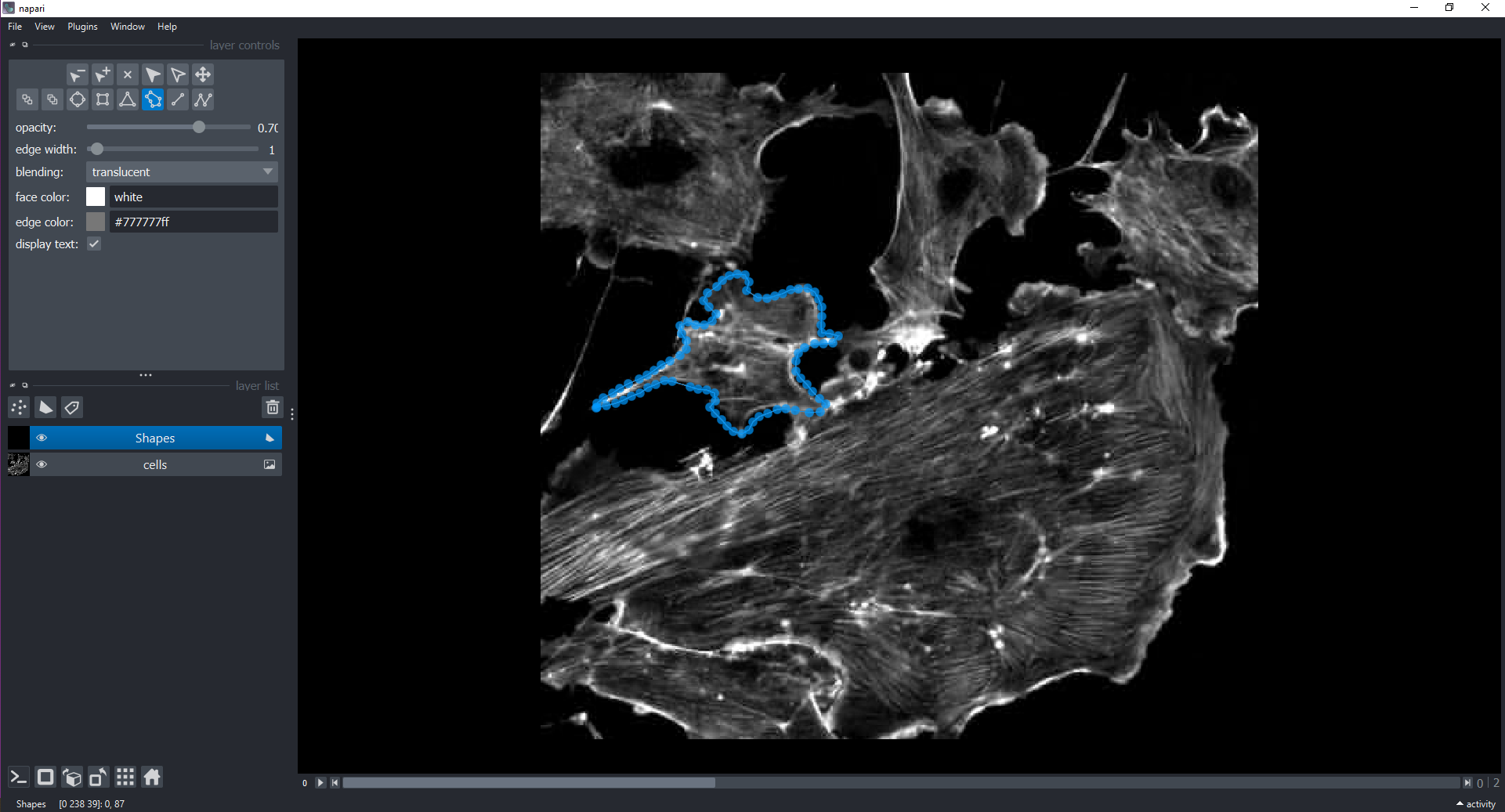

Using Napari as an image viewer (20 min)

In the Capstone challenge episode you made a function to count the number of bacteria colonies in an image also producing a new image that highlights the colonies. Modify this function to make use of Napari, as opposed to Matplotlib, to display both the original colony image and the segmented individual colonies. Test this new function on "data/colonies-03.tif". If you did not complete the Capstone challenge epsidode you can start with function from the solution. Hints:

A napari.Viewer object should be passed to the function as an input parameter.
The original image should be added to the Viewer as an Image Layer.
The labelled colony image should be to the Viewer as an Label Layer.

Show me the solution

Your new function might look something like this:

PYTHON

def count_colonies_napari(image_filename, viewer, sigma=1.0, min_colony_size=10, connectivity=2):
  bacteria_image = iio.imread(image_filename)
  gray_bacteria = ski.color.rgb2gray(bacteria_image)
  blurred_image = ski.filters.gaussian(gray_bacteria, sigma=sigma)

  # create mask excluding the very bright pixels outside the dish
  # we dont want to include these when calculating the automated threshold
  mask = blurred_image < 0.90
  # calculate an automated threshold value within the dish using the Otsu method
  t = ski.filters.threshold_otsu(blurred_image[mask])
  # update mask to select pixels both within the dish and less than t
  mask = np.logical_and(mask, blurred_image < t)
  # remove objects smaller than specified area
  mask = ski.morphology.remove_small_objects(mask, min_size=min_colony_size)

  labeled_image, count = ski.measure.label(mask, return_num=True)
  print(f"There are {count} colonies in {image_filename}")

  # add the orginal image (RGB) to the Napari Viewer
  viewer.add_image(data=bacteria_image, name="bacteria", rgb=True)
  # add the labeled image to the Napari Viewer
  viewer.add_labels(data=labeled_image, name="colony masks")

To run this function on "data/colonies-03.tif":

PYTHON

viewer.layers.clear()  # or viewer = napari.Viewer() if you want a new Viewer
count_colonies_napari(image_filename="data/colonies-03.tif", viewer=viewer)

OUTPUT

There are 260 colonies in data/colonies-03.tif

Learning to use the Napari GUI (optional, not included in timing)

Take some time to further familiarize yourself with the Napari GUI. You could load some of the course images and experiment with different features, or alternatively you could take a look at the official Viewer tutorial.

Napari plugins

Plugins extend Napari’s core functionally and allow you to add lots of cool and advanced features. There is an ever-increasing number of Napari plugins which are available from the Napari hub. For example:

napari-animation for making video annotations with key frames.
napari-segment-blobs-and-things-with-membranes for adding common image processing operations to the Tools menu.
napari-skimage-regionprops for measuring the properties of connected components from Label Layers.
napari-pyclesperanto-assistant for GPU-accelerated image processing operations.
napari-clusters-plotter for clustering objects according to their properties including dimensionality reduction techniques like PCA and UMAP.
napari-acceleration-pixel-and-object-classification for Random Forest-based pixel and object classification.
cellpose-napari and stardist-napari for pretrained deep learning-based models to segment cells and nuclei.
napari-n2v for self-supervised deep learning-based denosing.
napari-assistant, a meta-plugin for building image processing workflows.

Getting help on image.sc

image.sc is a community forum for all software-oriented aspects of scientific imaging, particularly (but not limited to) image analysis, processing, acquisition, storage, and management. Its great place to get help and ask questions which are either general or specific to a particular tool. There are active sections for python, scikit-image and Napari.

Processing 3D volumetric data

Recall that 3D volumetric data consists of an ordered sequence of images, or slices, each corresponding to a specific axial position. As an example lets work with skimage.data.cells3d()which is a 3D fluorescence microscopy image stack. From the dataset documentation we can see that the data has two channels (0: membrane, 1: nuclei). The dimensions are ordered (z, channels, y, x) and each voxel has a size of (0.29 0.26 0.26) microns. A voxel is the 3D equivalent of a pixel and the size specifies the physical dimensions, in (z, y, x) order for this example. Note the size of the voxels in z ( axial) is larger than the voxel spacing in the xy dimensions (lateral). Let’s load the data and visualise with Napari:

PYTHON

cells3d = ski.data.cells3d()
viewer.layers.clear()
viewer.add_image(data=cells3d, name=["membrane", "nucleus"], channel_axis=1)
print(cells3d.shape)

OUTPUT

(60, 2, 256, 256)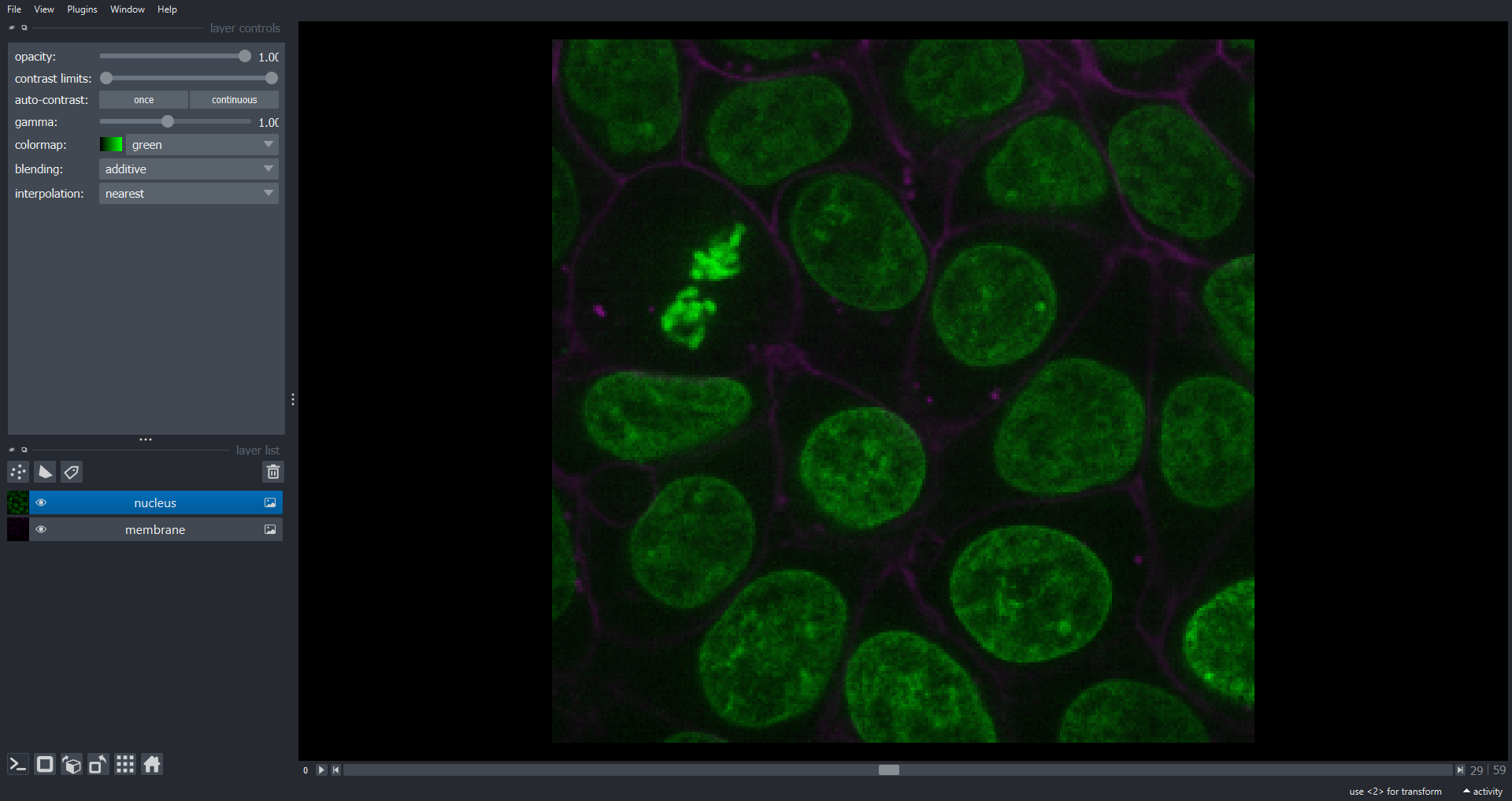

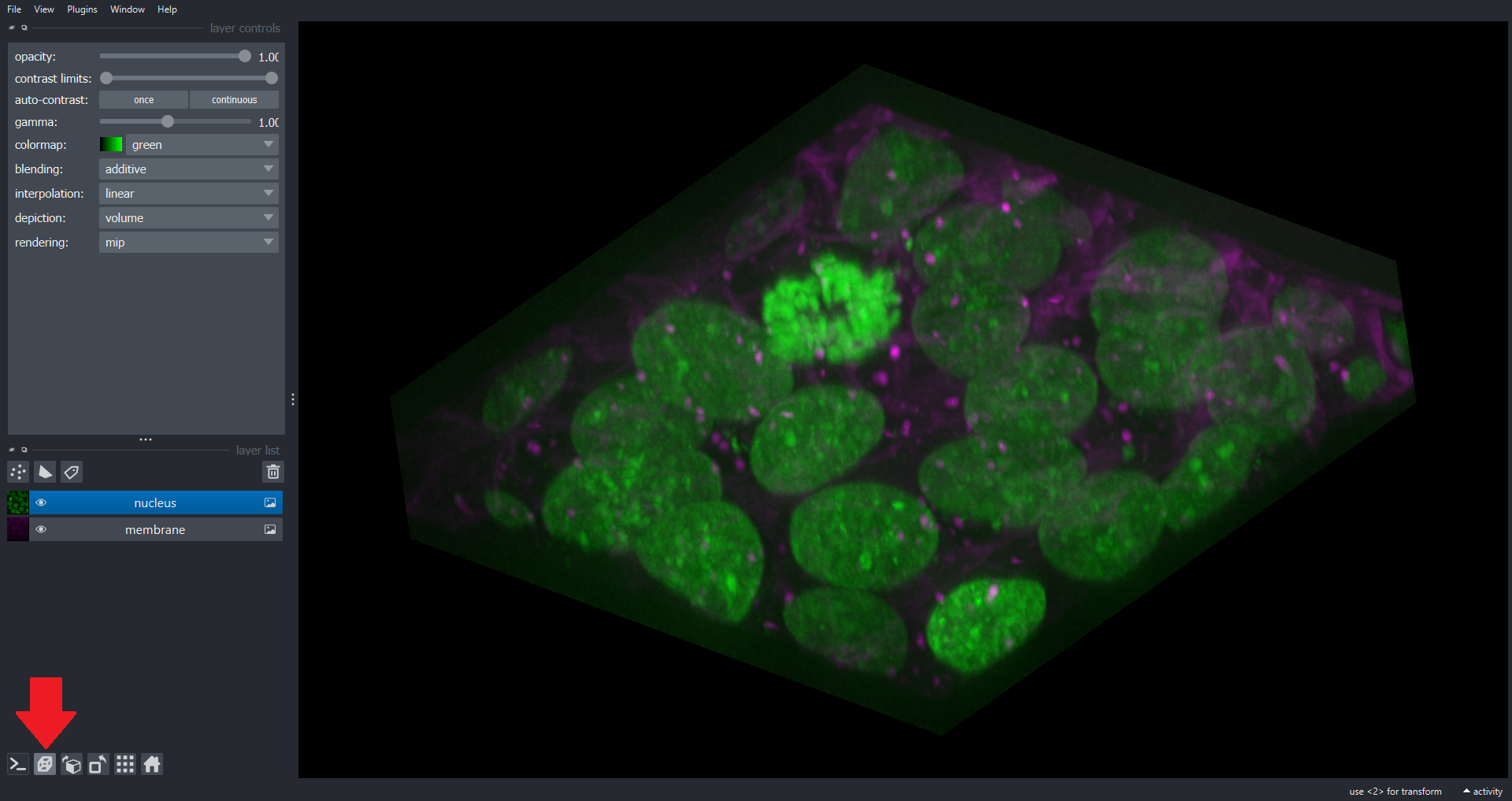
Note we now have a dimension slice to control which slice we are visualizing. You can also switch to a 3D rendering of the data:

Many of the scikit-image functions you have used throughout this Lesson work with 3D (or indeed nD) image data. For example lets blur the nuclei channel using a 3D Gaussian filter and add the result as a Image Layer to the Viewer:

PYTHON

# extract the nuclei channel
nuclei = cells3d[:, 1, :, :]
# store the voxel size as a NumPy array (in microns)
voxel_size = np.array([0.29, 0.26, 0.26])
# get sigma (std) values for each dimension that corresponds to 0.5 microns
sigma = 0.5 / voxel_size
# blur data with 3D Guassian filter
blurred_nuclei = ski.filters.gaussian(nuclei, sigma=sigma)
# add to Napari Viewer
viewer.add_image(data=blurred_nuclei, name="nucleus_blurred")
print(sigma)

OUTPUT

[1.72413793 1.92307692 1.92307692]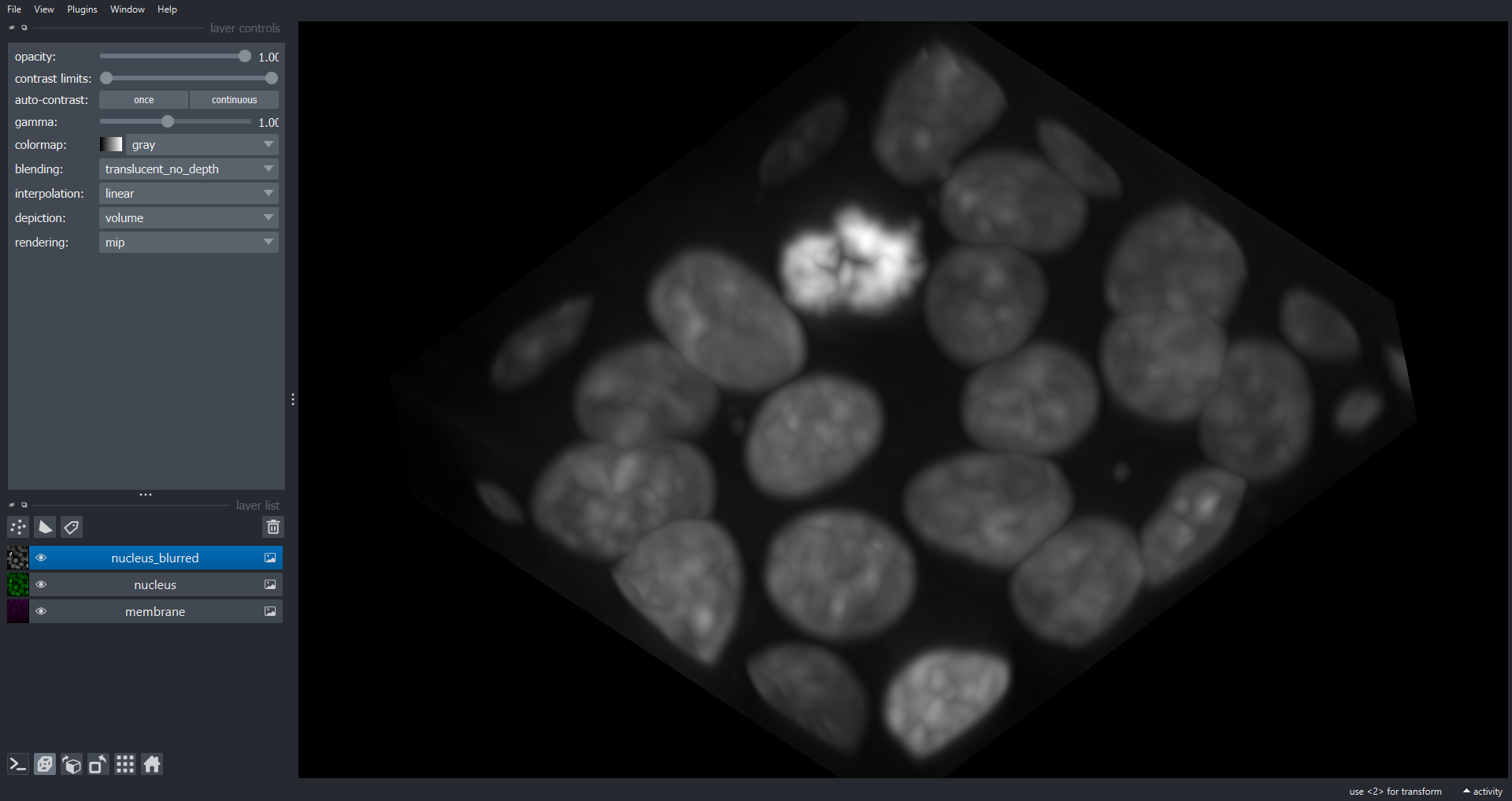

Note we have used a different sigma for the z dimension to allow for the different voxel dimensions, to produce a blur of 0.5 microns in each axis of real space. space.

Segmenting objects in 3D (25 min)

Write a workflow which:

Segments the nuclei within skimage.data.cells3d() to produce a 3D labelled volume.
Add the 3D labelled volume to a Napari Viewer as a Label Layer.
Calculate the mean volume in microns^3 of all distinct objects (connected components) in your 3D labelled volume.

You will need to recall concepts from the Thresholding and the Connected Components Analysis episodes. Hints:

The 3D blurred nuclei volume we have just calculated makes a good starting point.
ski.morphology.remove_small_objects() is useful for removing small objects in masks. In 3D the min_size parameter specifies the minimum number of voxels a connected component should contain.
In 3D we typically use connectivity=3 (as opposed to connectivity=2 for 2D data).
ski.measure.regionprops() can be used to calulate the properties of connected components in 3D. The returned "area" property gives the volume of each object in voxels.

Show me the solution

Starting with the 3D blurred nuclei volume as our starting point here is one potential solution that will segment the nuclei and add to the existing Napari Viewer:

PYTHON

# use an automated Otsu threshold to produce a binary mask of the nuceli
t = ski.filters.threshold_otsu(blurred_nuclei)
nuclei_mask = blurred_nuclei > t
# remove objects from the mask smaller than 5 microns^3
# np.prod(voxel_size) returns the volume of a voxel in microns^3
min_size = 5 / np.prod(voxel_size)
nuclei_mask = ski.morphology.remove_small_objects(nuclei_mask, min_size=min_size, connectivity=3)
# label 3D connected components
# we specify connectivity=3 but this is the default behaviour for 3D data
nuclei_labels = ski.measure.label(nuclei_mask, connectivity=3, return_num=False)
# add to Napari Viewer
viewer.add_labels(data=nuclei_labels, name="nuclei_labels")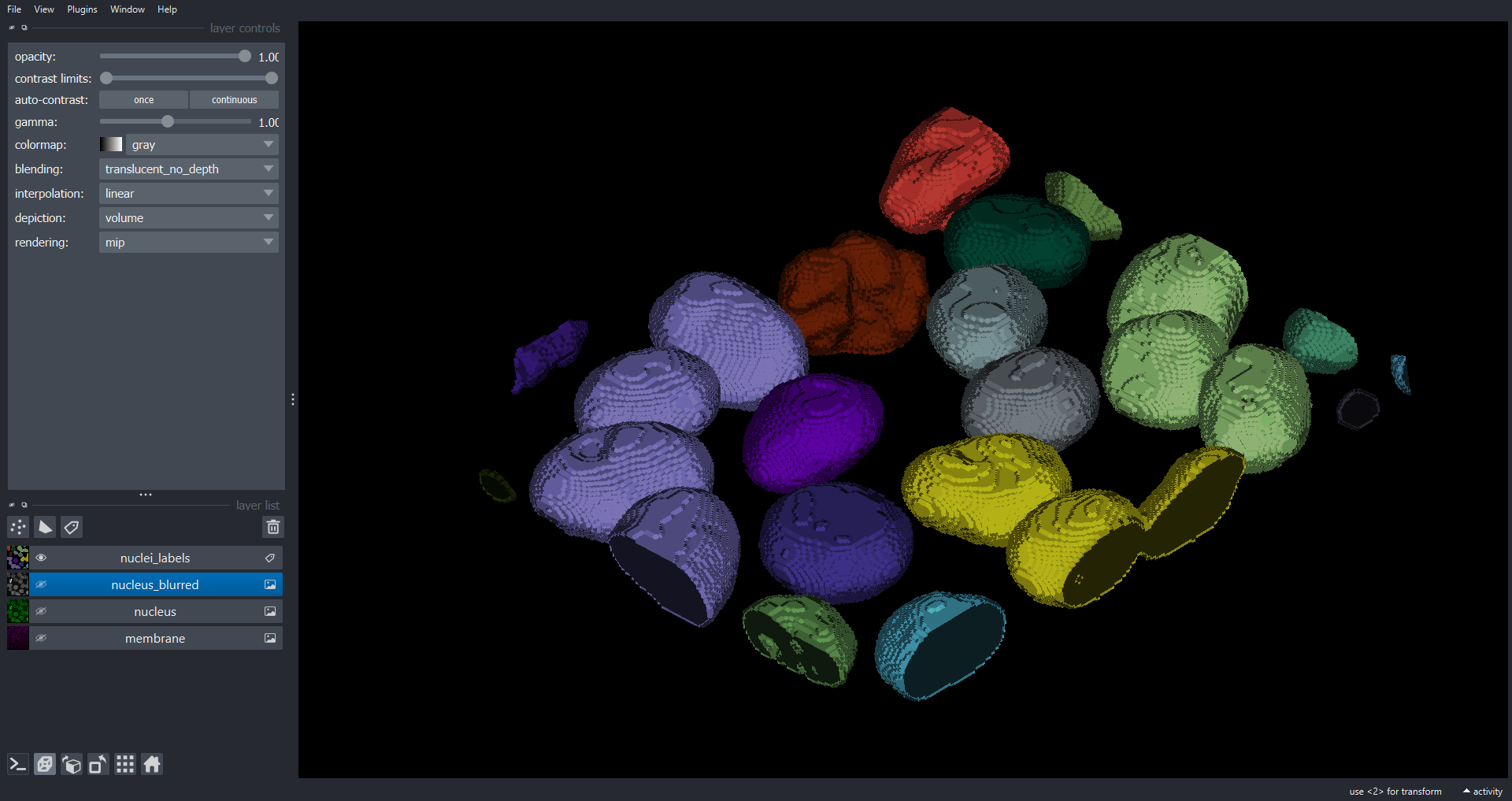

To extract the properties of the connected components we can use ski.measure.regionprops():

PYTHON

props = ski.measure.regionprops(nuclei_labels)
# get the cell volumes in pixels as a NumPy array
cell_volumes_voxels = np.array([objf["area"] for objf in props])
# get the mean and convert to microns^3
cell_volumes_mean = np.mean(cell_volumes_voxels) * np.prod(voxel_size)
f"There are {len(cell_volumes_voxels)} distinct objects with a mean volume of {cell_volumes_mean} microns^3"

OUTPUT

'There are 18 distinct objects with a mean volume of 784.6577237777778 microns^3'

Intensity morphometrics (optional, not included in timing)

It is common to want to retrieve properties of connected components which use the pixel intensities from the original data. For example the mean, max, min or sum pixel intensity within each object. Modify your solution from the previous exercise to also retrieve the mean intensity of the original nuclei channel within each connected component. You may need to refer to the ski.measure.regionprops() documentation.

Show me the solution

PYTHON

props = ski.measure.regionprops(nuclei_labels, intensity_image=nuclei)
# get the cell volumes in pixels as a NumPy array
cell_volumes_pixels = np.array([objf["area"] for objf in props])
# get the mean and convert to microns^3
cell_volumes_mean = np.mean(cell_volumes_pixels) * np.prod(voxel_size)
# mean intensity within each object
cell_mean_intensities = np.array([objf["intensity_mean"] for objf in props])
f"There are {len(cell_volumes_pixels)} distinct objects with a mean volume of {cell_volumes_mean} microns^3 and a mean intensity of {np.mean(cell_mean_intensities)}"

OUTPUT

'There are 18 distinct objects with a mean volume of 784.6577237777778 microns^3 and a mean intensity of 13876.25671914064'

Processing timelapse movies

Timelapse data consists of an ordered series of images, or frames, where each image corresponds to a specific point in time. data/cell_timelapse.tif is a timelapse fluorescence microscopy movie of cell nuclei with 41 timepoints. There are two cells at the beginning of the timelapse which both divide, via a process called mitosis, leaving fours cells at the end. Let’s load the data and visualise with Napari:

PYTHON

cell_timelapse = iio.imread(uri="data/cell_timelapse.tif")
viewer.layers.clear()
viewer.add_image(data=cell_timelapse, name="timelapse")
print(cell_timelapse.shape)

OUTPUT

(41, 113, 101)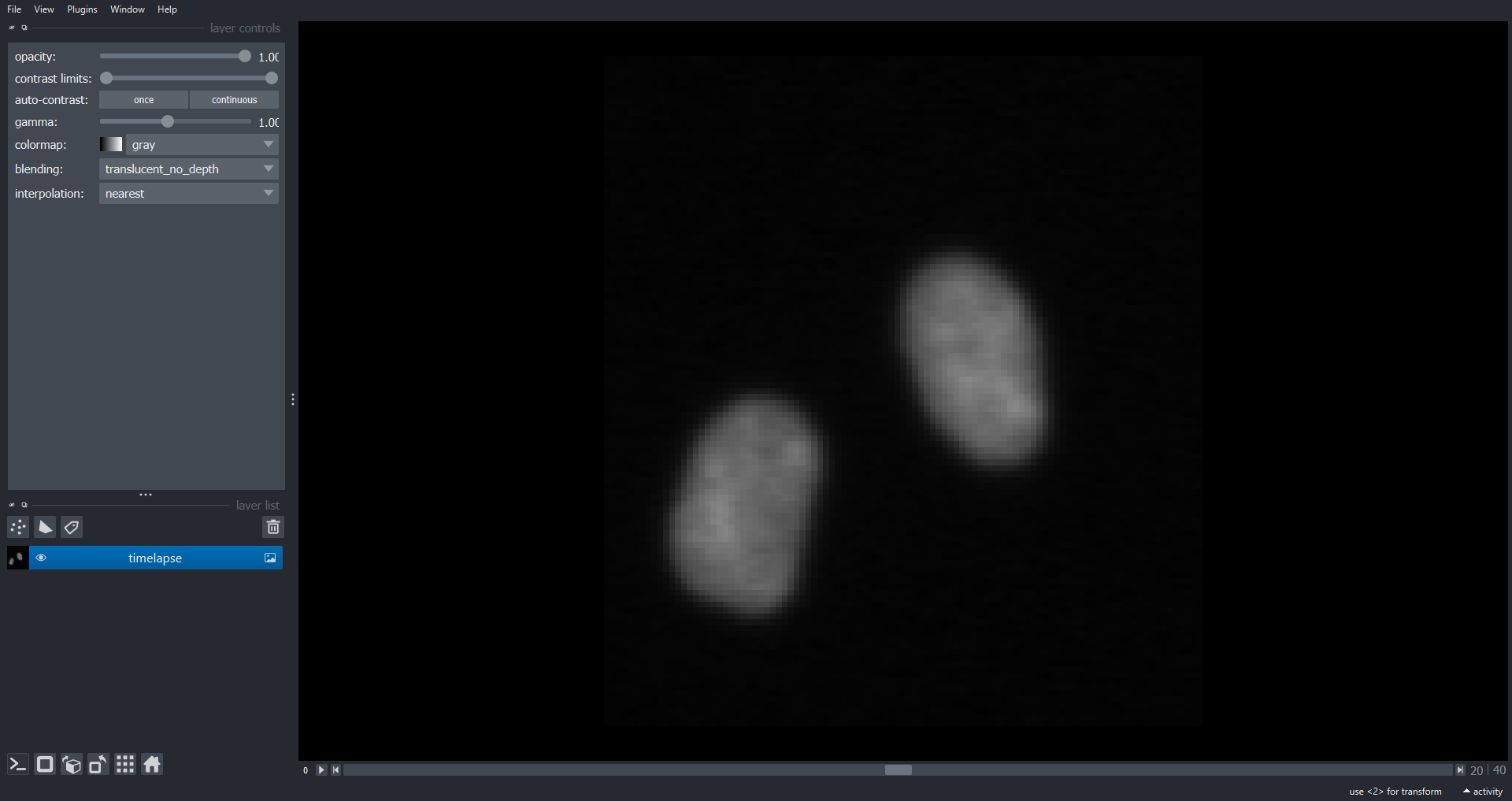

Note there is a dimension slider to navigate between timepoints and a playback button to play/pause the movie. When analysing timelapse data we can use our now familiar image processing functions from scikit-image. However, unlike volumetric data it is often appropriate to analyse each timepoint separately as 2D images rather than performing operations on the 3D NumPy array. To do this we can use a loop to iterate through timepoints. For example lets calculate the mean intensity of each frame in the timelapse and plot the results:

PYTHON

# empty list to store frame intensitys
mean_intensities = []
# loop through frames 
# enumerate gives convenient access to both the frame index and the frame
for frame_index, frame in enumerate(cell_timelapse):
  frame_mean = np.mean(frame)
  # add frame mean to list
  mean_intensities.append(frame_mean)

fig, ax = plt.subplots()
plt.plot(mean_intensities)
plt.xlabel("Timepoint")
plt.ylabel("Mean frame intensity")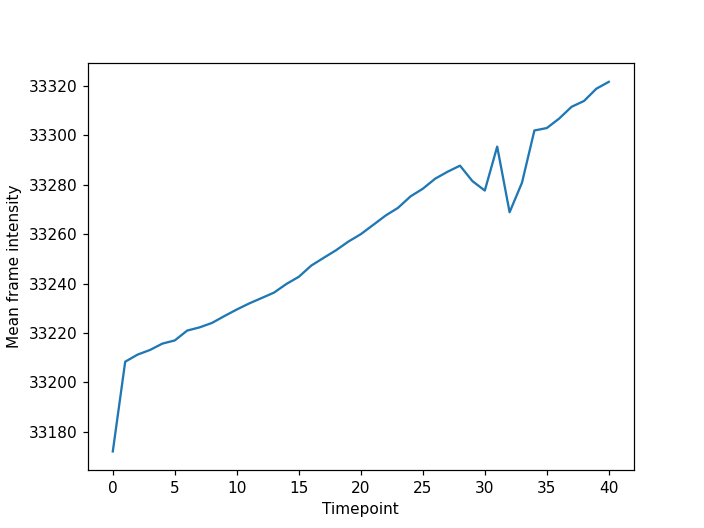

We can see that the frame intensity trends up throughout the movie with dips around timepoint thirty which if you look corresponds to when the cell divisions are occurring.

Calculating nuclear area over time (25 min)

Create a binary mask (3D boolean NumPy array) segmenting the nuclei in data/cell_timelapse.tif over time and add this mask to the Napari Viewer. You do not need to indentify/label individual objects/nuclei. Record the total area of the nuclei in each frame over time and plot the results. Hints:

Use a for loop to iterate through timepoints so you can process each frame separately.
You may find it useful to create a NumPy array for the binary mask (mask = np.zeros(cell_timelapse.shape, dtype=bool)). This array should be created outside the loop and filled in within it.

Show me the solution

Here is one potential solution:

PYTHON

# empty list for nuclear areas
nuclear_areas = []
# boolean mask for nuclear mask
# same shape as original timelapse
mask = np.zeros(cell_timelapse.shape, dtype=bool)

# iterate through timepoints
for frame_index, frame in enumerate(cell_timelapse):
  # blur the frame to reduce noise
  blurred_frame = ski.filters.gaussian(frame, sigma=1)
  # threshold with an Otsu approach
  t = ski.filters.threshold_otsu(blurred_frame)
  frame_mask = blurred_frame > t
  # fill in the corresponding frame of our global mask
  mask[frame_index] = frame_mask
  # append the area of the mask for this frame (the sum)
  nuclear_areas.append(np.sum(frame_mask))

# add mask to Napari Viewer
viewer.add_labels(data=mask, name="nuclear mask")

# plot the nuclear area over time
fig, ax = plt.subplots()
plt.plot(nuclear_areas)
plt.xlabel("Timepoint")
plt.ylabel("Total nuclear area")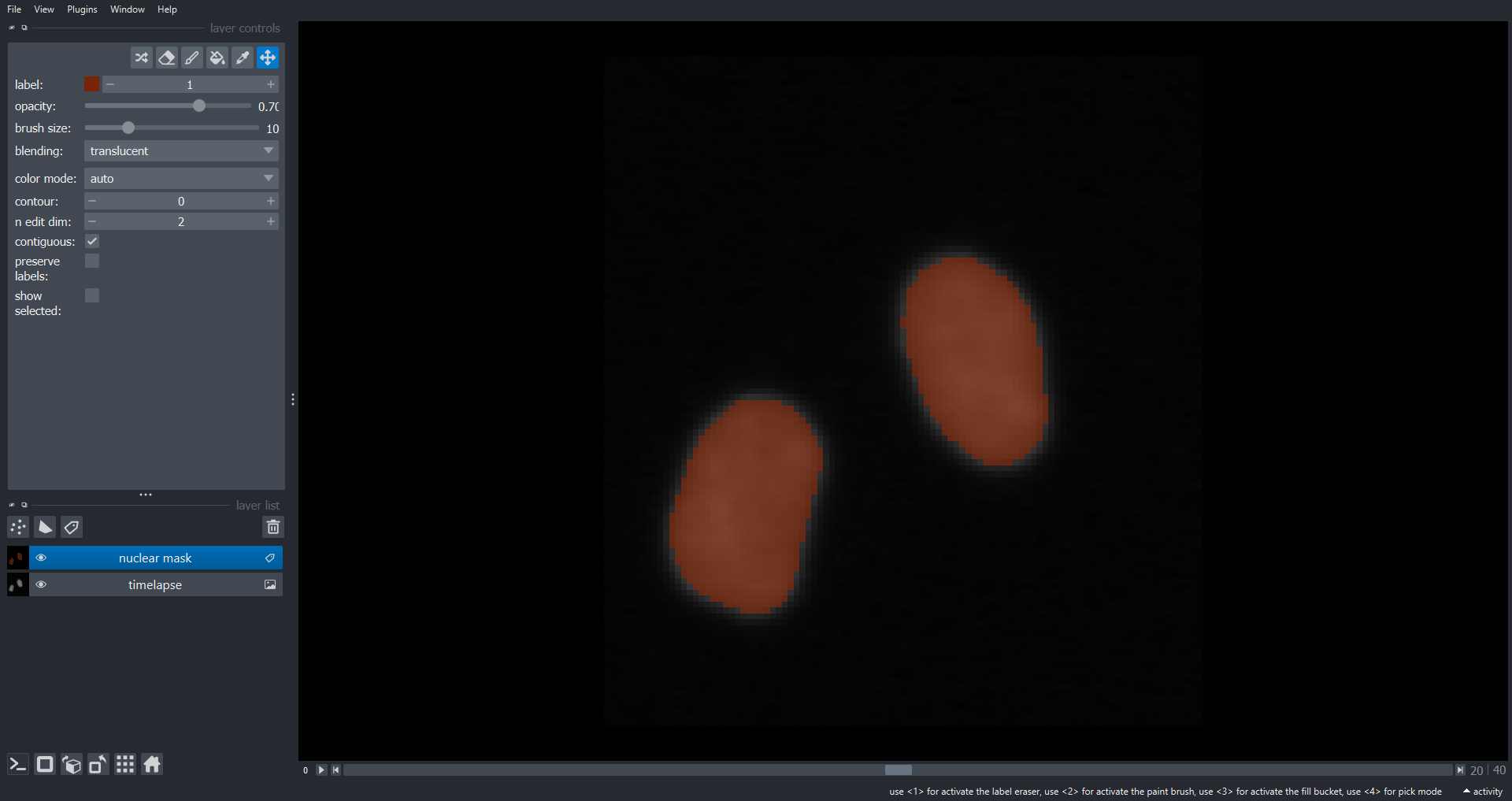

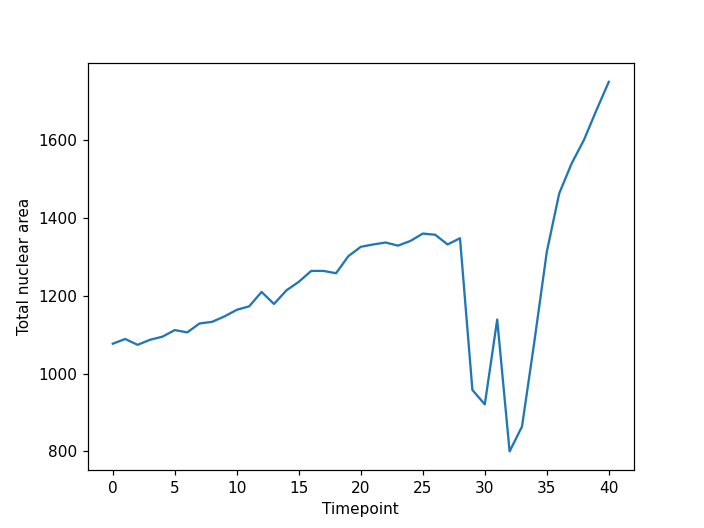
Note the two large drops in area around timepoint thirty corresponding the division events.

Tracking objects over time (optional, not included in timing)

Tracking is the process of following the trajectories of individual objects as they move over time. A simple approach to tracking is to find connected components in a timelapse treating the data as a 3D volume. This works well if the objects in question are well separated and do not move sufficiently far between timepoints to break the connectivity of the 3D (2D + time) connected component. Implement this approach for data/cell_timelapse.tif and plot the area of each object/nucleus as it changes over time. How well does this approach work? Do you think it would be sufficient for more complex data?

Show me the solution

Here is a potential solution:

PYTHON

# boolean mask for nuclear mask
# same shape as original timelapse
mask = np.zeros(cell_timelapse.shape, dtype=bool)
mask = np.zeros(cell_timelapse.shape, dtype=bool)

# iterate through timepoints
for time_index, frame in enumerate(cell_timelapse):
  # blur the frame to reduce noise
  blurred_frame = ski.filters.gaussian(frame, sigma=1)
  # threshold with an Otsu approach
  t = ski.filters.threshold_otsu(blurred_frame)
  frame_mask = blurred_frame > t
  # fill in the corresponding frame of our global mask
  mask[time_index] = frame_mask

# find the objects (connected components) in the 3D (2D + time) mask
labeled_mask, num_ccs = ski.measure.label(mask, connectivity=3, return_num=True)
# add labeled objects to Napari Viewer 
viewer.add_labels(data=labeled_mask, name="labeled_mask")

# plot for area of each object over time
fig, ax = plt.subplots()
plt.xlabel("Timepoint")
plt.ylabel("Nuclear area")
# iterate through objects
for label_index in range(num_ccs):
  # empty list for area of this object (nucelus) over time
  nuclear_area = []
  # iterate through timepoints and retrieve object areas
  for time_index, frame in enumerate(labeled_mask):
    nuclear_area.append(np.sum(frame == label_index + 1))
  # add line to plot for this object (nucelus)
  plt.plot(nuclear_area)

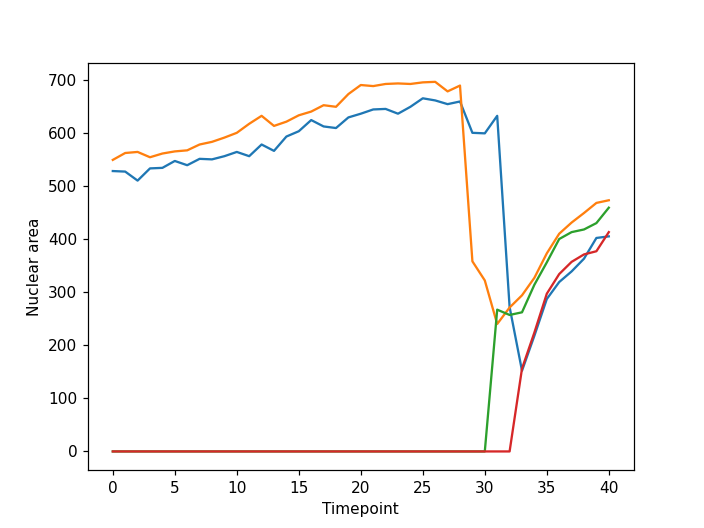
From the plot we can see our approach has worked well for this simple example. The movie starts with two nuclei which undergo division such that we have four nuclei at the end of the timelapse. However, for more complex data our simple tracking approach is likely to fail. If you are interested in tracking a good starting point could be a Napari plugin such as btrack which uses a Bayesian approach to track multiple objects in crowded fields of views.

Key Points

We can access open a Napari n-dimensional image viewer with viewer = napari.Viewer().
Image and Label Layers can be added to a viewer with viewer.add_image() and viewer.add_labels() respectively.
Many scikit-image functions such as ski.filters.gaussian(), ski.threshold.threshold_otsu(), ski.measure.label() and ski.measure.regionprops() work with 3D image data.
We can iterate through time-points to analyse timelapse movies.